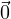 , all lines in ℝ2 containing the origin,
and ℝ2.
, all lines in ℝ2 containing the origin,
and ℝ2.The three must-haves for a subspace V are:
Show that the subspaces of ℝ2 are precisely 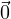 , all lines in ℝ2 containing the origin,
and ℝ2.
, all lines in ℝ2 containing the origin,
and ℝ2.
The three must-haves for a subspace V are:
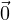 ∈ V
∈ V
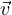 ∈ V
∈ V 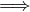 c
c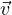 ∈ V
∈ V
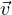 ∈ V,
∈ V,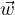 ∈ V
∈ V 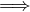
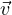 +
+ 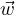 ∈ V
∈ V In plain prose, the zero vector must be included in the set (i). An element of the set
multiplied by any scalar must also be in the set (ii). And the set must be closed
under addition (i.e., the sum of any two elements in the set must also be in the set)
(iii).
So, clearly, the zero vector 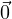 by itself is a subspace of ℝ2. (We note that any scalar c
times
by itself is a subspace of ℝ2. (We note that any scalar c
times 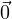 still equals
still equals 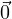 for Rule (ii), and that
for Rule (ii), and that 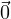 +
+ 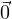 =
= 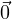 for Rule (iii).) So, what about
the other two examples?
for Rule (iii).) So, what about
the other two examples?
Well, note that a general element of ℝ2 is a vector with two entries that looks
like:

where a,b ∈ ℝ. So we take this arbitrary element 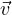 from ℝ2 and an arbitrary
element c from the field we are working with (the reals, ℝ) and take their product,
corresponding with Rule (ii):
from ℝ2 and an arbitrary
element c from the field we are working with (the reals, ℝ) and take their product,
corresponding with Rule (ii):
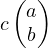
But doesn’t this look familiar? It’s a parametric description of a line that
crosses through the origin, aka a line with direction vector  , where c can
vary freely over the reals! Let’s quickly check our rules: for Rule (i), simply
let c = 0. 0
, where c can
vary freely over the reals! Let’s quickly check our rules: for Rule (i), simply
let c = 0. 0 =
= 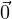 , so the zero vector is included, perfect. Rule (iii) is
vacuously true because we are only considering one element from ℝ2 at a
time.
, so the zero vector is included, perfect. Rule (iii) is
vacuously true because we are only considering one element from ℝ2 at a
time.
Okay, let’s deal with the last instance of a subspace: ℝ2 itself. How does this
work?
Well, in our last example, we considered only one element from ℝ2, so how about we
now look at two elements:
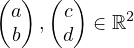
Let’s take their linear combination:
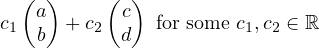
Then, let’s assume that  and
and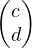 are linearly independent; that is, they
cannot be expressed in terms of each other. We need to assume this because
otherwise, if they were linearly dependent, their sum would just be a line and we
would be back in our previous case.
are linearly independent; that is, they
cannot be expressed in terms of each other. We need to assume this because
otherwise, if they were linearly dependent, their sum would just be a line and we
would be back in our previous case.
So in other words, we are looking at the span of  and
and 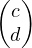 . But we know that
the span of any two linearly independent vectors in ℝ2 must be a space of dimension
2; in other words, it must span the whole of ℝ2.
. But we know that
the span of any two linearly independent vectors in ℝ2 must be a space of dimension
2; in other words, it must span the whole of ℝ2.
Let’s quickly check our rules. We can quickly confirm that our set of vectors includes
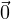 by letting c1 = c2 = 0:
by letting c1 = c2 = 0:
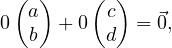
which fulfills Rule (i). We check that an arbitrary scalar k times any element of our set is still in the set:
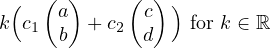
Well, since k,c1,c2 are all arbitrary scalars, we can let d1 = kc1 and d2 = kc2 and rewrite our equation like this:
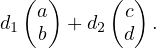
Well, what do you know—this is precisely the general form of an element in our
set, so we know that this resulting element must also be in the set. Rule (ii)
proved!
For Rule (iii), we take two arbitrary elements and look at their sum:
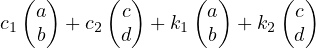
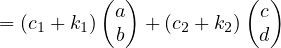
If we let e1 = c1 + k1 and e2 = c2 + k2, then the above expression can be written as:
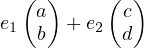
and it follows that this resulting sum still belongs to our set. That was tedious, but now we are pretty much done.
Let U = 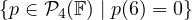 . Find a basis of U.
. Find a basis of U.
Axler uses the notation 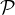 m(F) to define the set of polynomials up to degree m with
coefficients in F. (Because I’m lazy and boring, I’m going to assume that F here is
just ℝ.) So,
m(F) to define the set of polynomials up to degree m with
coefficients in F. (Because I’m lazy and boring, I’m going to assume that F here is
just ℝ.) So, 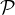 m(F) = Span(1,z,z2,z3,z4)
m(F) = Span(1,z,z2,z3,z4)
Anyways…what does the set 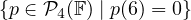 look like? From the way it’s
defined, it might sound a little abstract. But since we know that p(6) = 0 we can say
that:
look like? From the way it’s
defined, it might sound a little abstract. But since we know that p(6) = 0 we can say
that:
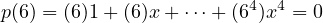
where 0 here represents the zero polynomial, or the polynomial whose coefficients are all 0. So now we have that:
| a0 | = -a16 - a2(62)x - a 3(63)x2 - a 4(64)x3 | ||
| = -a16 - a236x1 - a 3216x2 - a 41296x3 |
And we plug this back in for the general form of p(x):
| p(x) | = (-a16 - a236x - a3216x2 - a 41296x3) + a 1x + a2x2 + a 3x3 + a 4x4 | ||
| = a1(x - 6) + a2(x2 - 36x) + a 3(x3 - 216x2) + a 4(x4 - 1296x3) |
Now it’s much easier to see that the polynomials:
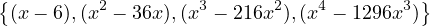
span the space 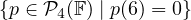 . This set is also linearly independent, which
makes it a basis.
. This set is also linearly independent, which
makes it a basis.
Extend the basis in (a) to a basis of 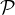 4(F).
4(F).
So 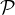 4(F) has dimension 5. All we need to do is add an element to what we got in
(a), since dimension of a space is defined as the length of the basis of that
space:
4(F) has dimension 5. All we need to do is add an element to what we got in
(a), since dimension of a space is defined as the length of the basis of that
space:
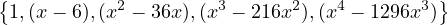
That’s 5 things, right? And they’re all linearly independent right? Yay.
Find a subspace W of  4(F) such that
4(F) such that  4(F) = U ⊕ W.
4(F) = U ⊕ W.
Very related to part (b), since we have a basis of  4(F) in terms of the basis
of our original set mentioned in the problem description, we can just use
the subspace
4(F) in terms of the basis
of our original set mentioned in the problem description, we can just use
the subspace 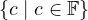 (which would represent the first term in the basis
(which would represent the first term in the basis
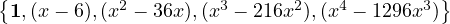 ).
).
Let U = 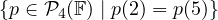 . Find a basis of U.
. Find a basis of U.
Okay, things should go more smoothly now that I have a handle on polynomials as
vector spaces. I HOPE. Let’s set the general forms of p(2) and p(5) in ℙ4(F) equal to
each other:
| p(2) | = a0 + 2a1 + 4a2 + 8a3 + 16a4 | ||
| = a0 + 5a1 + 25a2 + 125a3 + 625a4 | |||
| = p(5) |
Let us compress this into something more informative…
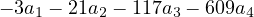
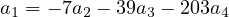
Okay now we write this in terms of a general element of 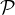 4(F):
4(F):
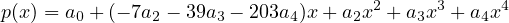
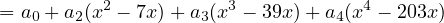
There’s our basis!
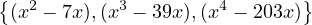
Extend the basis in (a) to a basis of 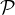 4(F).
4(F).
I’m not sure if I’m a total idiot and completely misunderstanding this question,
because this seems too easy, but my answer is always going to be:
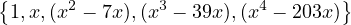
Like come on that’s gotta be at least close.
Find a subspace W of 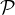 4(F) such that
4(F) such that 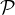 4(F) = U ⊕ W.
4(F) = U ⊕ W.
Well, this is the subspace spanned by 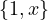 . Let’s write it out: Span
. Let’s write it out: Span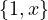 lol. Lmao.
I realise now that I could’ve solved part (a) with a system of linear equations, in the
true spirit of linear algebra. Oh well.
lol. Lmao.
I realise now that I could’ve solved part (a) with a system of linear equations, in the
true spirit of linear algebra. Oh well.
Let U = 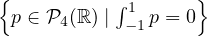 . Find a basis of U.
. Find a basis of U.
Oh, what the hell. An integral? I haven’t seen those in…a whole academic year. I’m
basically a helpless deer in headlights now. I mean, ummmm this predicate
evaluates to true for odd functions. I THINK that’s actually the definition for
an odd function. And the only polynomials in 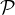 4(F) that are odd are x
and x3. I’m not going to lie to you, despite my authoritative(?) tone in the
index of my website I actually have no idea what I’m doing most of the
time.
4(F) that are odd are x
and x3. I’m not going to lie to you, despite my authoritative(?) tone in the
index of my website I actually have no idea what I’m doing most of the
time.
I wonder if the basis is just:
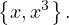
You know the math walkthrough is going to be amazing when the phrase “I wonder” pops up on like the third question. BUT IT MAKES SENSE I SWEAR I mean I’m just thinking about how the sum and the difference of two odd functions is also odd. It just werks.
Extend the basis in (a) to a basis of 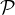 4(ℝ).
4(ℝ).
We have to add 1,x2, and x4 to get our beloved standard basis again:
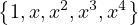
I dunno why I wrote it all out. I don’t know why I do anything at all.
Find a subspace W of 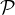 4(ℝ) such that
4(ℝ) such that 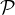 4(ℝ) = U ⊕ W.
4(ℝ) = U ⊕ W.
A polynomial centered at the origin is either odd or even. So oddness and evenness
are two mutually exclusive and exhaustive traits. So I will be picking the naive and
obvious answer as I usually do and make W be the set of even polynomials of
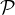 m(F). I don’t know how to write that in set-builder notation. Something
like
m(F). I don’t know how to write that in set-builder notation. Something
like
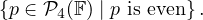
Which also is the subspace spanned by 1,x2,x4 :)
Suppose m is a positive integer and p0,p1,…,pm ∈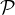 (F) are such that each pk has
degree k. Prove that p0,p1,…,pm is a basis of
(F) are such that each pk has
degree k. Prove that p0,p1,…,pm is a basis of 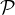 m(F).
m(F).
To prove that a set forms a basis of a space, you have to prove that the set is
linearly independent and that it spans the whole space. Without further
ado:
All proofs of linear independence follow about the same framework. Set the linear combination to 0, and prove that for that to be the case, all the coefficients must equal 0. So something like this:

Where
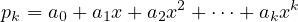
for ak≠0. I mean, I guess you could say that each term pi is its own sum where
the last term is some coefficient times xi. That must be the case, since ai≠0. So this
just means that we can’t express any p1 in terms of the other pis, i.e., we can
never be able to express anything of the form x2 in terms of x or x3. And so
on.
I guess I could try to make this argument more rigorously, like setting
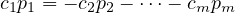
And then, again, since we know that p1 at least has the term aixi that’s non-zero, we can divide by p1:
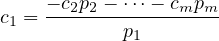
Dividing pk by p1 is just gonna produce another polynomial pk-1 (I HOPE):
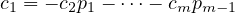
Since the expression on the left c1 is of degree 0, and all the terms on the right
hand side have degrees of at least 1, then it follows that the only way for the above
equality to hold is if c2 =  = cm = 0. You can do this for the rest of the coefficients
and I really hope that the polynomials with negative degrees don’t mess things
up.
= cm = 0. You can do this for the rest of the coefficients
and I really hope that the polynomials with negative degrees don’t mess things
up.
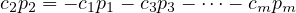
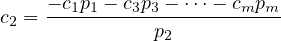
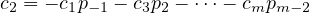
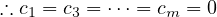
After all that, we STILL have half the proof to do. I don’t know why I’m doing this,
reader. Why I’m spending the last night of this weekend slaving over proofs that
should be trivial when I could be uhhhh I could be doing ummmm uhhhh
yeah
For proofs of spanning you typically want to look at the coordinates or entries, but
these aren’t vectors so let’s try and find something analogous. I mean, I guess you
could look at entries of a vector as being analogous to the nth degree term of a
polynomial?
But you could also take the standard basis of 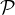 m(F), which is
m(F), which is 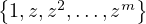 .
And in our case, we can treat p0,p1,…,pm to be identical to z0,z1,…,zm. This is
probably too cursory. This is probably cope. But I mean intuitively, p0,…,pm must
span
.
And in our case, we can treat p0,p1,…,pm to be identical to z0,z1,…,zm. This is
probably too cursory. This is probably cope. But I mean intuitively, p0,…,pm must
span 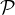 m(F). Right???
m(F). Right???
Suppose U and W are both four-dimensional subspaces of ℂ6. Prove that there exist
two vectors in U ∩ W such that neither of these vectors is a scalar multiple of the
other.
Okay this looks pretty straightforward. So take the standard basis of ℂ6, and I’m
going to write it all out because I hate myself:
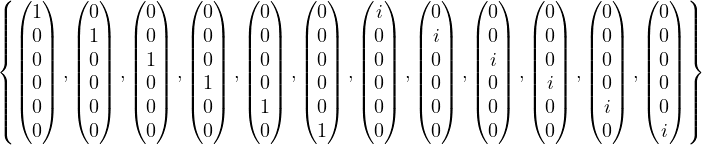
Since dimU = dimW = 4, this means the basis of U and the basis of W are lists
with length at most 4 (by defn of basis/dimension).
I’m not going to lie to you, I’m not very familiar with complex vector spaces
so I’m going to take a rain check on this one. I WILL come back to this
though.
Suppose U and W are both five-dimensional subspaces of ℝ9. Prove that
U ∩ W≠ .
.
Oh thank god this is over the reals. Okay. PIGEONHOLE PRINCIPLE
TIME.
Theorem 1. If n items are put into m containers, with n > m, then at least one container must contain more than one item.
What does this have to do with anything, you ask? Well, take the standard basis of ℝ9, which is:
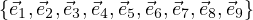
where 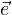 i is the vector ∈ ℝ9, with a 1 in the ith position and 0s everywhere
else.
i is the vector ∈ ℝ9, with a 1 in the ith position and 0s everywhere
else.
Okay that’s 9 things! And if U and W are five-dimensional, then their basis must
consist of 5 things from this set! This is like putting 9 objects into 5 slots. And since
9 is larger than 5 (just in case you didn’t know this fascinating fact), there must be a
slot that contains more than one object. In this case, the slot with more than one
object (vector) represents the intersection of U and W. Thus by the pigeonhole
principle, U ∩ W≠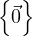 .
.
Suppose V is finite-dimensional and V 1,V 2,V 3 are subspaces of V with
dimV 1 + dimV 2 + dimV 3 > 2dimV . Prove that V 1 ∩ V 2 ∩ V 3≠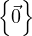 .
.
Ohhhh pigeonhole again. Which fills me with joy and love for all the denizens of the
Earth. Wait there’s no guarantee that V is over the reals. Wait what. Are we just
making a really general assumption here? Okay I guess then…
Suppose that dimV 1 + dimV 2 + dimV 3 > 2dimV . Then, it follows that
dimV 1 + dimV 2 + dimV 3 > dimV . Also, V 1,V 2,V 3 ⊂ V . So any element
in V 1,V 2, or V 3 must also be in V , or to put it another way, V contains
V 1,V 2,V 3.
But if dimV 1 + dimV 2 + dimV 3 > dimV , this means that the sum of the lengths of
the respective bases of V 1,V 2,V 3 is larger than the length of the basis of V (which
we know to be finite). But, we also know that V contains these three subspaces, so
the elements of the bases of V 1,V 2,V 3 must be elements from the basis of
V .
This is a restatement of the pigeonhole principle (m slots, n objects, n > m 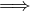 at
least one slot has more than one object). Thus, V 1 ∩ V 2 ∩ V 3 must have
some non-trivial overlap. I really hope this at least approximates a correct
answer.
at
least one slot has more than one object). Thus, V 1 ∩ V 2 ∩ V 3 must have
some non-trivial overlap. I really hope this at least approximates a correct
answer.
Suppose that V 1,…,V m are finite-dimensional subspaces of V . Prove that
V 1 +  + V m is finite-dimensional and
+ V m is finite-dimensional and
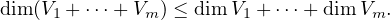
This is mildly interesting and OH YEAH I just remembered that this does have
an analogy which is called the union bound or something like that. I love
it when I can do less work. :D The smiley face honestly looks so derpy in
Computer Modern but you guys will be spared of it when I convert all of this to
HTML
Anyways
I was totally wrong and union bound only applies to measures. Actually maybe it
applies here in some sense but I’m definitely not sure. But, we can use another small
proof. Namely, I claim that the inequality |A∪B|≤|A| + |B| always holds. I also say
that to prove the original problem, it suffices to prove the inequality above always
holds.
This is because V 1 +  + V m is analogous to set unions. And by the principle of
inclusion-exclusion (PIE), |A∪B|≤|A| + |B|. So let’s prove this. A quick proof
by cases:
+ V m is analogous to set unions. And by the principle of
inclusion-exclusion (PIE), |A∪B|≤|A| + |B|. So let’s prove this. A quick proof
by cases:
Case 1: A and B are disjoint, i.e, A∩B = ∅, and |A∩B| = 0. So, |A∪B| = |A| + |B|
and we’re done. The subspace version of this is supposing that V i,V j are disjoint, so
dimV i + V j = dimV i + dimV j.
Case 2: A and B aren’t disjoint. WLOG, have A \ B ∪ B. We know for sure that
A \ B and B are disjoint, so |A \ B ∪ B| = |A \ B| + |B|. And since |A \ B| < |A|
(since we are assuming A ∩ B≠∅), it follows that |A \ B ∪ B| < |A| + |B|.
The subspace version of this is that V i ∩V j≠ , so WLOG there are some vectors
in V i that lie in the span of the basis of V j. So, when we take their sum and
find its basis, we discard some redundant vectors (otherwise we wouldn’t
have a linearly independent set of vectors, and thus no longer a basis). So,
dimV i + V j < dimV i + dimV j.
, so WLOG there are some vectors
in V i that lie in the span of the basis of V j. So, when we take their sum and
find its basis, we discard some redundant vectors (otherwise we wouldn’t
have a linearly independent set of vectors, and thus no longer a basis). So,
dimV i + V j < dimV i + dimV j.
You can generalize this for any number of subspaces/sets which is what you do to
cultivate PIE to its true form in all its glory. Aaaand we’re done (or so I tell
myself).
Explain why you might guess, motivated by analogy with the formula for the number of elements in the union of three finite sets, that if V 1,V 2,V 3 are subspaces of a finite-dimensional vector space, then:
| dim(V 1 + V 2 + V 3) | = dimV 1 + dimV 2 + dimV 3 | ||
| - dim(V 1 ∩ V 2) - dim(V 1 ∩ V 3) - dim(V 2 ∩ V 3) | |||
| + dim(V 1 ∩ V 2 ∩ V 3) |
Then either prove the formula above or give a counterexample.
PIE will help us here. “Keep odds and throw out evens”. I will be right back as I am
lightheaded from hunger, and the mention of pie uhhhhhhh yeah let me define
this later. Okay I’m back with food and I’m so good at being a functional
person.
Although I kind of feel like I’m being hit by a truck now, I will forge onwards. So, I
might guess that this is the case because of PIE, and because when forming a basis
(to find the dimension), I want to throw out redundant elements (so that I maintain
linear independence). This explains the pairwise intersections being subtracted;
you don’t want to double-count a vector that pops up in the overlap of two
subspaces.
But the three-wise (trio-wise? trinity-wise? No) intersections, we want to add, to
compensate for our subtraction of the pairwise shared elements (the three-wise
shared elements will be subtracted twice—excessively so).
Proof. We want to show that dim(V 1+V 2+V 3) = dimV 1+dimV 2+dimV 3-
dim(V 1 ∩ V 2) - dim(V 2 ∩ V 3) - dim(V 1 ∩ V 3) + dim(V 1 ∩ V 2 ∩ V 3).
Let the basis of V 1 be represented  , the basis of V 2 be
, the basis of V 2 be  ,
and V 3’s basis be
,
and V 3’s basis be 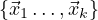 . Note that we are making no assumptions about
the exact value of the dimension of V 1,V 2, or V 3.
. Note that we are making no assumptions about
the exact value of the dimension of V 1,V 2, or V 3.
Note that any element 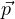 ∈ V 1+V 2+V 3 can be written as a sum of the bases of
V 1,V 2,V 3. In order to construct this new basis, we take the union of the basis
of each individual subspace, like:
∈ V 1+V 2+V 3 can be written as a sum of the bases of
V 1,V 2,V 3. In order to construct this new basis, we take the union of the basis
of each individual subspace, like:
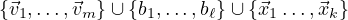
. When taking this union, it’s important to discard elements that appear in
pair-wise intersections in order to maintain linear independence. More tangibly,
when we have 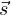 i = c
i = c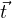 j for some scalar c, with
j for some scalar c, with 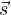 ∈ V m and
∈ V m and 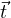 ∈ V n, we discard
one of these elements from the union.
∈ V n, we discard
one of these elements from the union.
But simply keeping the elements that appear in V 1,V 2,V 3 and constructing a
linearly independent set out of those elements is not sufficient. We need to add
back in the elements that appear in all three of the subspaces in order to ensure
that our set spans—these elements were thrown out during our consideration of
the pairwise intersections. Then, we finally reach the form of the equation given
in the problem statement. __
So, that was pretty character-building. When I say “character-building” I usually mean painful, both physically and mentally. I’ve been sitting down for too long. Let me stand up and walk around so I feel like a human again. Thanks for reading.