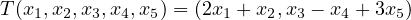
Give an example of a linear map T with dimnull T = 3 and dimrange T = 2.
Define a linear map T : ℝ5 → ℝ2 such that:
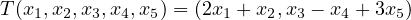
Then null T is the set of all elements of ℝ3 such that x1 = -1∕2x2, x3 = x4 - 3x5:
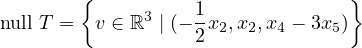
Thus, dimnull T = 3. Then, see that range T is the set of all vectors of form:
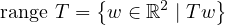
Thus, dimrange T = 2. Then, by the fundamental theorem of linear maps, it makes sense that the dimension of the domain, ℝ5, is 2 + 3 = 5.
Proof. Suppose S,T ∈ (V ) are such that range
(V ) are such that range 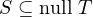 . Prove that
. Prove that
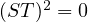 .
.
Suppose that 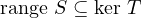 . Then, for all
. Then, for all 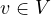 ,
, 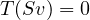 (*). We see
that:
(*). We see
that:
| (ST)2v | = ST(STv) | ||
| = S(TS)(Tv) (by associativity of linear maps) | |||
| = S0 (by (*)) | |||
| = 0 (by definition of linear map) |
Thus 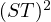 is equivalent to the zero map, as we wanted to show. __
is equivalent to the zero map, as we wanted to show. __
Suppose 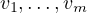 is a list of vectors in
is a list of vectors in 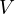 . Define
. Define 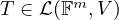 by
by
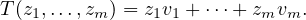
What property of 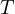 corresponds to
corresponds to 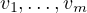 spanning
spanning 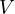 ?
?
For v1,…,vm to span V , we want range T = V . This is precisely the definition of T
being surjective.
What property of 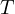 corresponds to the list
corresponds to the list 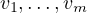 being linearly
independent?
being linearly
independent?
For v1,…,vm to be linearly independent, we want for a linear combination of
v1,…,vm, with coefficients a1,…,am ∈ F:
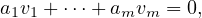
and we require that a1 =  = am = 0. But note that this is equivalent
to:
= am = 0. But note that this is equivalent
to:
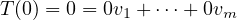
where the zeroes in the first and second expressions are the list of length m whose
entries are all 0, and the zeroes in the linear combinations are simply scalars. In other
words, we require for null T = 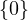 . But this is precisely the definition of T being
injective. Thus, the property of T that corresponds to the list v1,…,vm being linearly
independent is injectivity.
. But this is precisely the definition of T being
injective. Thus, the property of T that corresponds to the list v1,…,vm being linearly
independent is injectivity.
Show that 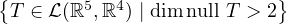 is not a subspace of
is not a subspace of  (ℝ5, ℝ4).
(ℝ5, ℝ4).
For dimnull T > 2 to hold, we look to the fundamental theorem of linear
maps:
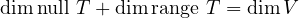
We know that dimV = 5, and that dimrange T = 4. So, by the fundamental
theorem, we know that dimnull T = dimV - dimrange T = 5 - 4 = 1. So, the
set defined as 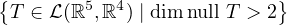 is actually the empty set,
∅.
is actually the empty set,
∅.
Give an example of T ∈ (ℝ4) such that range T = null T.
(ℝ4) such that range T = null T.
Define a linear transformation T ∈ (ℝ4):
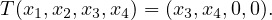
Then, range T = Span
 ,
,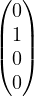
 , and dimnull T = Span
, and dimnull T = Span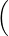
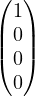 ,
,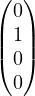
 .
To put it more clearly, any vector of the form (a1,a2,0,0), when put through the
linear transformation T, will become (0,0,0,0) (since the first two entries are
“discarded” by T). But, the range of T is precisely those vectors of the form
(b1,b2,0,0).
.
To put it more clearly, any vector of the form (a1,a2,0,0), when put through the
linear transformation T, will become (0,0,0,0) (since the first two entries are
“discarded” by T). But, the range of T is precisely those vectors of the form
(b1,b2,0,0).
Also see that dimrange T = dimnull T = 2, and that dimrange T +dimnull T = 2+2 = 4,
which is what we expect (since the domain is ℝ4).
It’s worth mentioning that I didn’t get this immediately, nor on my first try. I started
by playing around with 2 × 2 examples of matrices (cheating a bit, since in Axler’s
book, we haven’t quite gotten around to connecting linear transformations to
matrices). My math professor constantly says that creating small examples
is very important in gaining intuition to solve a more general problem, a
piece of advice that (to my chagrin, sometimes) holds true in basically any
scenario.
Prove that there does not exist T ∈ (ℝ5) such that range T = null T.
(ℝ5) such that range T = null T.
This actually holds true for any linear transformation that can be encoded as a
square matrix with odd dimensions. We can look at it that way (which is slightly
more concrete and familiar to me), or, we can look at it through the lens of the
fundamental theorem of linear maps, which is probably what Axler wants us to do
here…
So we just plug in appropriate values into the fundamental theorem. This is relevant
because for range T to equal null T, their dimensions surely must be equal. So we
have:
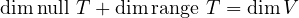

where dimnull T = dimrange T. Do you see the issue here? 5 is an odd number,
and yet according to our equation above, we need a positive integer (let’s call it x)
such that 2x = 5. But this is impossible.
Thus, there does not exist T ∈ (ℝ5) such that range T = null T.
(ℝ5) such that range T = null T.
Suppose V and W are finite-dimensional with 2 ≤ dimV ≤ dimW. Show that
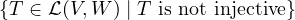 is not a subspace of
is not a subspace of  (V,W).
(V,W).
If T ∈ (V,W) and T is not injective, then T must map to a space of strictly lesser
dimension; i.e., dimV > dimW. Suppose that V,W are finite-dimensional and
dimV ≤ dimW. So the set
(V,W) and T is not injective, then T must map to a space of strictly lesser
dimension; i.e., dimV > dimW. Suppose that V,W are finite-dimensional and
dimV ≤ dimW. So the set 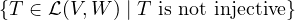 is in fact empty and
therefore is not a subspace of
is in fact empty and
therefore is not a subspace of  (V,W).
(V,W).
Suppose V and W are finite-dimensional with dimV ≥ dimW ≥ 2. Show that
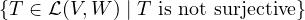 is not a subspace of
is not a subspace of  (V,W).
(V,W).
Similarly to Exercise 7, we use the fact that if T ∈ (V,W) and T is not surjective,
then T must map to a space of strictly higher dimension; i.e., dimV < dimW. But
we suppose that V,W are finite-dimensional and that dimV ≥ dimW. So,
(V,W) and T is not surjective,
then T must map to a space of strictly higher dimension; i.e., dimV < dimW. But
we suppose that V,W are finite-dimensional and that dimV ≥ dimW. So,
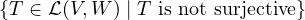 is empty and therefore not a subspace of
is empty and therefore not a subspace of
 (V,W).
(V,W).
Suppose T ∈ (V,W) is injective and v1,…,vn is linearly independent in V . Prove
that Tv1,…,Tvn is linearly independent in W.
(V,W) is injective and v1,…,vn is linearly independent in V . Prove
that Tv1,…,Tvn is linearly independent in W.
If T ∈ (V,W) and T is injective, then Tv = Tw implies v = w for v,w ∈ V . Suppose
that the list of vectors v1,…,vn is linearly independent in V . We wish to
show that Tv1,…,Tvn is linearly independent in W, so we set up a linear
combination:
(V,W) and T is injective, then Tv = Tw implies v = w for v,w ∈ V . Suppose
that the list of vectors v1,…,vn is linearly independent in V . We wish to
show that Tv1,…,Tvn is linearly independent in W, so we set up a linear
combination:
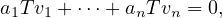
and we wish to show that for the above equality to hold, a1 =  = an, all
elements of F, must all be 0.
= an, all
elements of F, must all be 0.
But we know that v1,…,vn is linearly independent in V :
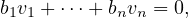
and all b1,…,bn ∈ F must equal 0. Set these two linear combinations equal to each other:
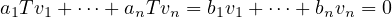
Let’s set all other coefficients aside from a1,b1 to zero:
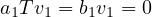
Since v1,…,vn is a linearly independent list, we know that v1 must be some
non-zero element of V , so for this equality to hold, it is clear that b1 = 0. Further,
since we know that T is injective, the only vector that is mapped to the zero vector is
the zero vector itself. Seeing that v1 is a non-zero vector, we can assume that
Tv1 is also non-zero, which forces a1 to equal 0. We repeat this process for
aiTvi and bivi, for i = 2,…,n, showing that at each step, ai must equal
0.
We have shown for the linear combination
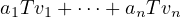
to equal 0, a1 =  = an must all be 0. And since Tv1,…,Tvn ∈ W, we have
shown that Tv1,…,Tvn is linearly independent in W.
= an must all be 0. And since Tv1,…,Tvn ∈ W, we have
shown that Tv1,…,Tvn is linearly independent in W.
Suppose v1,…,vn spans V and T ∈ (V,W). Show that Tv1,…,Tvn spans
range T.
(V,W). Show that Tv1,…,Tvn spans
range T.
The range of a linear transformation is the subset of W consisting of those vectors
that are equal to Tv for some v ∈ V . But note that any arbitrary vector v ∈ V can be
expressed as a linear combination of v1,…,vn. So let v = c1v1 +  + cnvn for some
scalars c1,
+ cnvn for some
scalars c1, ,cn ∈ F. Then Tv = T(c1v1 +
,cn ∈ F. Then Tv = T(c1v1 +  + cnvn. By linearity, this results
in:
+ cnvn. By linearity, this results
in:
| Tv | = T(c1v1 +  + cnvn) + cnvn) | ||
= Tc1v1 +  + Tcnvn + Tcnvn | |||
= c1Tv1 +  + cnTvn + cnTvn |
If any element of range T can be written as a linear combination of Tv1,…,Tvn, then it follows that Tv1,…,Tvn spans range T.
Suppose that V is finite-dimensional and that T ∈ (V,W). Prove that there exists a
subspace U of V such that:
(V,W). Prove that there exists a
subspace U of V such that:

Written in plain English, the only vector in common to U and null T is the zero vector, and the range of T are all Tu where u is an element of U. We take a look at our reliable rank-nullity theorem:
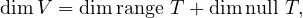
and find that the constraints imposed on us earlier are quite possible, if we let
dimnull T = 0, and dimrange T = dimV .
This can be done by letting dimnull T = 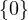 (a quirk that is worth mentioning: the
set which only contains the zero vector is considered to have dimension 0). This
forces dimrange T = dimV , as we mentioned before. And since U is a subspace of V ,
we have a stronger argument: if U is a subspace of V and dimU = dimV , then
U = V .
(a quirk that is worth mentioning: the
set which only contains the zero vector is considered to have dimension 0). This
forces dimrange T = dimV , as we mentioned before. And since U is a subspace of V ,
we have a stronger argument: if U is a subspace of V and dimU = dimV , then
U = V .
So, yes, there does exist a subspace U of V such that those conditions are met: U
must be V itself.
Suppose T is a linear map from F4 to F2 such that:
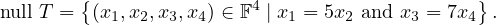
Prove that T is surjective.
Since T is a linear map from F4 to F2 (i.e., a linear map from a higher- to a
lower-dimensional subspace), we can be certain that it can be surjective in the first
place. So, to continue with proving that T is surjective, it is a matter of showing that
range T = F2.
First, let’s take a closer look at what the above equation is telling us: that all vectors
in F4 of the form (5x2,x2,7x4,x4), are sent to 0 by the linear transformation T. How
many vectors does it take to span this space? It takes two: a potential basis could be
(5,1,0,0) and (0,0,7,1).
Note that the rank-nullity theorem tells us then that dimrange T = 2. This is what
we wanted to show, since this implies that range T = F2.
Suppose U is a three-dimensional subspace of ℝ8 and that T is a linear map from ℝ8
to ℝ5 such that null T = U. Prove that T is surjective.
Suppose U ⊂ ℝ3 and dimU = 3. Suppose also that T is defined as a linear map
T : ℝ8 → ℝ5 such that null T = U. We want to show that range T = ℝ5.
The rank-nullity theorem tells us that:
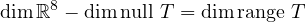
We plug in the values that we already have:
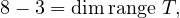
so we know that dimrange T = 5. This suffices to show that dimrange T = F5. Thus, T is surjective.
Prove that there does not exist a linear map from F5 to F2 whose null space equals
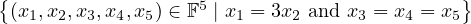 .
.
Suppose such a linear map exists, and let it be defined T : F5 → F2. A closer look at
the null space of T as described shows that all vectors in F5 of the form
(3x2,x2,x3,x3,x3) are sent to 0 by T. Since there are only two “free” variables in
(3x2,x2,x3,x3,x3), we know that null T can be spanned by two linearly independent
vectors; that is, dimnull T = 2.
By the rank-nullity theorem:

(This is just another way to write the same thing we already have been writing; Ker referring to null and Im referring to range.) Plugging in our known values, we get the equation:
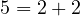
which is clearly a contradiction. Thus, no such linear map can exist.
Suppose there exists a linear map on V whose null space and range are both
finite-dimensional. Prove that V is finite-dimensional.
This immediately follows from the rank-nullity theorem. If the null space and range
of a linear map over V are finite-dimensional, then the dimension of V is the sum of
the dimension of the null space and range; the sum of two finite numbers will always
be another finite number.
Suppose V and W are finite-dimensional. Prove that there exists an injective linear
map from V to W iff dimV ≤ dimW.
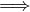 : Suppose T ∈
: Suppose T ∈ (V,W) and that T is injective. We know that for this to be the
case, dimV ≤ dimW. (3.22)
(V,W) and that T is injective. We know that for this to be the
case, dimV ≤ dimW. (3.22)
 : Suppose dimV ≤ dimW. Suppose T is a linear map from V to W, but note
that we aren’t making any assumptions about whether it is injective or otherwise
(yet!). By the rank-nullity theorem:
: Suppose dimV ≤ dimW. Suppose T is a linear map from V to W, but note
that we aren’t making any assumptions about whether it is injective or otherwise
(yet!). By the rank-nullity theorem:
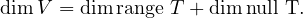
For T to be injective, we know that null T must be 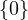 , i.e., dimnull T = 0. Note
that range T ⊂ W, so dimrange T ≤ dimW. We express this inequality in the
theorem above, along with our claim that dimnull T should be zero:
, i.e., dimnull T = 0. Note
that range T ⊂ W, so dimrange T ≤ dimW. We express this inequality in the
theorem above, along with our claim that dimnull T should be zero:
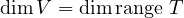
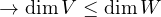
This is precisely the condition we assumed at the beginning. Thus, we have shown that if dimV ≤ dimW, there exists an injective linear map from V to W. (At least, I hope we did. I easily get confused when writing iff proofs.)
Suppose W is finite-dimensional and T ∈ (V,W). Prove that T is injective iff there
exists S ∈
(V,W). Prove that T is injective iff there
exists S ∈ (W,V ) such that ST is the identity operator on V .
(W,V ) such that ST is the identity operator on V .
 : Suppose T ∈
: Suppose T ∈ (V,W) is injective. We wish to show that there exists
S ∈
(V,W) is injective. We wish to show that there exists
S ∈ (W,V ) such that ST is the identity operator on V . If T is injective, then
null T =
(W,V ) such that ST is the identity operator on V . If T is injective, then
null T = 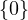 ; i.e., the only vector that is sent to 0 by T is the zero vector itself.
Further, T maps distinct inputs to distinct outputs. If v,w ∈ V and v≠w, then
Tv≠Tw.
; i.e., the only vector that is sent to 0 by T is the zero vector itself.
Further, T maps distinct inputs to distinct outputs. If v,w ∈ V and v≠w, then
Tv≠Tw.
So, it follows that there exists an S ∈ (W,V ) that takes distinct Tv and
Tw, etc, back to v,w, etc. If this is the case, then ST essentialy maps v
to v and w to w, which is precisely the definition of the identity operator.
(W,V ) that takes distinct Tv and
Tw, etc, back to v,w, etc. If this is the case, then ST essentialy maps v
to v and w to w, which is precisely the definition of the identity operator.
 : Suppose there exists S ∈
: Suppose there exists S ∈ (V,W) such that ST is the identity operator on
V . We wish to show that T ∈
(V,W) such that ST is the identity operator on
V . We wish to show that T ∈ (V,W) is injective. If the composition of
two linear maps, S and T, results in the identity operator, this means that
S is the inverse mapping of T. Therefore, T is invertible. Therefore, T is
injective.
(V,W) is injective. If the composition of
two linear maps, S and T, results in the identity operator, this means that
S is the inverse mapping of T. Therefore, T is invertible. Therefore, T is
injective.
This is too verbose and hand-wavy, even for my taste. I probably will edit
this later.
Suppose V is finite-dimensional, T ∈ (V,W), and U is a subspace of W. Prove that
(V,W), and U is a subspace of W. Prove that
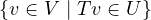 is a subspace of V and:
is a subspace of V and:
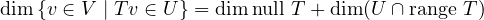
Intuitively, the set 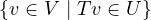 is talking about the subset of V such that it
contains all the elements in V that are being mapped to U by T. So, we should just
check the usual subspace conditions:
is talking about the subset of V such that it
contains all the elements in V that are being mapped to U by T. So, we should just
check the usual subspace conditions:
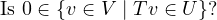
Yes, any linear map from V to W sends the 0 in V to the 0 in W.
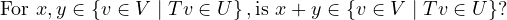
Let p,q ∈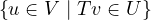 . So, looking at p,q from the point of view
of the subspace U, we note that p + q would be of the form Tp + Tq, and
by linearity, could be written T(p + q). So p + q is clearly an element of
. So, looking at p,q from the point of view
of the subspace U, we note that p + q would be of the form Tp + Tq, and
by linearity, could be written T(p + q). So p + q is clearly an element of
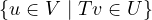 .
.
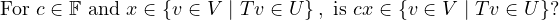
Similarly, take cx ∈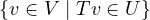 , and rewrite it as T(cx). See that it could
be written (by linearity) as cTx, so cx is clearly an element of
, and rewrite it as T(cx). See that it could
be written (by linearity) as cTx, so cx is clearly an element of 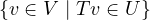 .
.
For the second part of this proof, we have to show something related to dimensions,
so let’s consult our trusty rank-nullity theorem, which says the dimension of the
domain of a linear map is the sum of the dimension of the null space and the
dimension of the range of the linear map. But the set 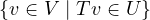 is only
considering a subset of the domain of T.
is only
considering a subset of the domain of T.
range T is defined to be all those elements in W that are “hit” by the linear map T.
This set may be larger than U, since U is a subspace of W. But U is closely
connected to the subspace of V , 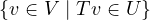 , because this set describes those
elements in v that get mapped to elements in U by T. Further, U ∩ range T is
describing the very set
, because this set describes those
elements in v that get mapped to elements in U by T. Further, U ∩ range T is
describing the very set 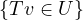 !
!
Then, it is clear that the dimension of 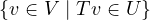 is the sum of the vectors
that are “lost”, i.e., sent to zero after T is applied, plus the dimension of the space
defined in the last paragraph (U ∩ range T).
is the sum of the vectors
that are “lost”, i.e., sent to zero after T is applied, plus the dimension of the space
defined in the last paragraph (U ∩ range T).
Suppose U and V are finite-dimensional vector spaces and S ∈ (V,W) and
T ∈
(V,W) and
T ∈ (U,V ). Prove that:
(U,V ). Prove that:
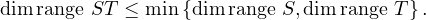
We see that ST describes a linear map from V to itself, i.e., ST ∈ (V ).
(V ).
By rank-nullity theorem, define dimrange S ≤ dimV . By similar logic,
dimrange ST ≤ dimV , so it follows that dimrange ST ≤ dimrange S.
Now we wish to show that dimrange ST ≤ dimrange T. Note that null T ⊂ null ST.
So, dimnull T ≤ dimnull ST. By the rank-nullity theorem, this shows that
dimrange ST ≤ range T.
Thus, dimrange ST ≤ min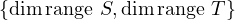 .
.
Suppose that W is finite-dimensional and S,T ∈ (V,W). Prove that null S ⊆ null T
iff there exists E ∈
(V,W). Prove that null S ⊆ null T
iff there exists E ∈ (W) such that T = ES.
(W) such that T = ES.
 : Suppose that for linear maps S and T, both from V to W (with W being
finite-dimensional), there exists a E ∈
: Suppose that for linear maps S and T, both from V to W (with W being
finite-dimensional), there exists a E ∈ (W) such that T = ES. We wish to show
that null S ⊆ null T.
(W) such that T = ES. We wish to show
that null S ⊆ null T.
Suppose that v ∈ V and v ∈ null S. Then, note that if Sv = 0 for some v ∈ V , then
(ES)v = E(Sv) = E(0) = 0, so v ∈ null T.
 : Suppose that null S ⊆ null T. We wish to show that there exists E ∈
: Suppose that null S ⊆ null T. We wish to show that there exists E ∈ (W)
such that T = ES.
(W)
such that T = ES.
Suppose that v ∈ null S, and that for all such v, v ∈ null T. We wish to
show that there exists E ∈ (W) such that T = ES. Does this not follow
from the fact that if w ∈ null S, then Sw = 0, and by extension Tw = 0?
Then, define a mapping E from W to W, so that T = ES, and use similar
reasoning from above to show that null S ⊂ null E. I’m pretty confused
with this part of the proof, if it wasn’t obvious. I’ll have to come back to
this.
(W) such that T = ES. Does this not follow
from the fact that if w ∈ null S, then Sw = 0, and by extension Tw = 0?
Then, define a mapping E from W to W, so that T = ES, and use similar
reasoning from above to show that null S ⊂ null E. I’m pretty confused
with this part of the proof, if it wasn’t obvious. I’ll have to come back to
this.
Also very verbose—my apologies. Although this one is somewhat more
focused/does a better job of explaining my thought process. Plus, it
actually arrives at a concrete answer.
Suppose P ∈ (V ) and P2 = P. Prove that V = null P ⊕ range P.
(V ) and P2 = P. Prove that V = null P ⊕ range P.
Whenever you see ⊕, it denotes a “direct sum”. The definition of a direct sum is
something I always have to look up and reconfirm for myself what it is, because it’s
simple enough for you to fool yourself. But it turns out it isn’t always so
easy, especially because a direct sum means something slightly different
depending on which mathematical object you’re summing over. Wow, there’s
nuance.
Anyways, a direct sum of two vector spaces, V ⊕ W, isn’t so bad. Suppose for any
x ∈ X, it can be uniquely expressed as x = x1 + x2 for x1 ∈ V and x2 ∈ W. Then
X = V ⊕ W. I suppose you could also look at it like this:
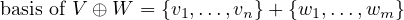
Where v1,…,vn is a basis of V and w1,…,wm is a basis of W. Okay, what else do
we know? Well, P is a linear transformation mapping elements of V to itself.
Interestingly enough, P2 = P, so applying P twice to v ∈ V produces the same result
as if you’d just applied it once. I guess this tells us something crucial: that
null P = 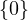 .
.
Intuitively, I know that this must be the case because the equality P2 = P tells me
that we don’t “lose” any vectors when we apply P. That is, at least when applied the
first and second time, P does not force any other vectors to go to 0 other than the
zero vector itself. If P did have a non-trivial null space, then P2 could never equal P;
the vectors that got sent to 0 on the first pass of P would then be lost forever.
Well, if null P = 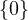 , then by the rank-nullity theorem, range P must span the
entire space of V , i.e., we know that range P ⊂ V , and that dimV = dimrange P, so
range P = V .
, then by the rank-nullity theorem, range P must span the
entire space of V , i.e., we know that range P ⊂ V , and that dimV = dimrange P, so
range P = V .
Then it follows that the direct sum of null P and range P is the uninteresting direct
sum of V and the zero vector, which is just…V .
Suppose p ∈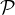 (ℝ). Prove that there exists a polynomial q ∈
(ℝ). Prove that there exists a polynomial q ∈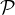 (ℝ) such that
5q′′ + 3q′ = p.
(ℝ) such that
5q′′ + 3q′ = p.
Axler does note here that this can be proved without linear algebra, but that “it is
more fun with linear algebra”. When I saw this question, my first instinct was to use
the fact that the differentiation map is almost surjective. Then I thought, what
would the integration map look like? (This question was probably irrelevant,
however)
Define the degree of p to be n, and consider the linear map:
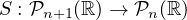
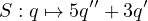
Now, all we have to do is show that S is surjective, because then that
would mean for all p ∈ n(ℝ), there is a mapping from q ∈
n(ℝ), there is a mapping from q ∈ n+1(ℝ) to p via
S.
n+1(ℝ) to p via
S.
For S to be surjective, we want its range to be  n(ℝ), so we want dimnull S = 1.
But considering that S is a differentiation map, we know that any element of null S
is simply a constant (the derivative of a constant is 0, the second derivative of a
constant is 0). So, dimnull S = 1.
n(ℝ), so we want dimnull S = 1.
But considering that S is a differentiation map, we know that any element of null S
is simply a constant (the derivative of a constant is 0, the second derivative of a
constant is 0). So, dimnull S = 1.
Now using our rank-nullity theorem:
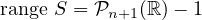
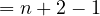
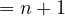
The subspace of 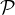 n(ℝ) with dimension n + 1 can only be
n(ℝ) with dimension n + 1 can only be 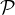 n(ℝ) itself. Thus,
we’ve proved that S is surjective, and we are done.
n(ℝ) itself. Thus,
we’ve proved that S is surjective, and we are done.
Suppose ϕ ∈ (V, F) and ϕ≠0. Suppose u ∈ V is not in null ϕ. Prove that
(V, F) and ϕ≠0. Suppose u ∈ V is not in null ϕ. Prove that
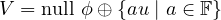
Direct sum again…okay, so if u ∈ V is not in null ϕ, then ϕ(u)≠0 by definition. In fact, any scalar multiplied by u is also not in null ϕ. This is due to the linearity of ϕ:
| ϕ(λu) | = λϕ(u) | ||
| = λ(0) | |||
| = 0 |
So, it follows that u and any scalar multiple of u is not in ϕ, which explains the
second term of the direct sum above, 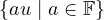 .
.
Further, note that the co-domain of ϕ is F. Then, dimrange ϕ ≤ 1. Since ϕ≠0,
dimϕ > 0, therefore dimrange ϕ = 1.
Let dimV = n. Then:
| dimnull ϕ | = dimV - dimrange ϕ | ||
| = dimV - 1 | |||
| = n - 1 |
Let a basis of null ϕ be v1,…,vn-1. We want to show that extending this basis by
the vector u (therefore resulting in the list of vectors v1,…,vn-1,u) gives a valid basis
for V . This suffices to show that V is a direct sum of null ϕ and 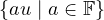 .
.
To show that v1,…,vn-1,u is a basis of V, we must show that this list is linearly
independent. To do so, we have our usual routine:
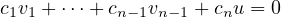
We claim that for the above equality to hold, all coeffs c1,…,cn must be
0.
We write:
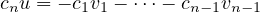
Which shows that since cnu can be written as a linear combination of the basis
vectors of null ϕ, cnu ∈ null ϕ. Since we know that u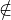 null ϕ, cn must be 0. But wait.
We have supposed that v1,…,vn-1 is a basis of null ϕ, so by definition they are
linearly independent. So, in order for the equality to hold, we have to have
c1 =
null ϕ, cn must be 0. But wait.
We have supposed that v1,…,vn-1 is a basis of null ϕ, so by definition they are
linearly independent. So, in order for the equality to hold, we have to have
c1 =  = cn-1 = 0.
= cn-1 = 0.
Since we have shown v1,…,vn-1,u to be linearly independent, we have proved that it
is a valid basis for V ; we are done.
Suppose V is finite dimensional, X is a subspace of V , and Y is a finite-dimensional
subspace of W. Prove that there exists T ∈ (V,W) such that null T = X and
range T = Y iff dimX + dimY = dimV .
(V,W) such that null T = X and
range T = Y iff dimX + dimY = dimV .
 : Suppose that dimX + dimY = dimV . We wish to show that there exists
T ∈
: Suppose that dimX + dimY = dimV . We wish to show that there exists
T ∈ (V,W) such that null T = X and range T = Y .
(V,W) such that null T = X and range T = Y .
I’m not sure how to solve this other than directly referencing dimX + dimY = dimW.
Help…
 : Suppose that there exists T ∈
: Suppose that there exists T ∈ (V,W) such that null T = X and range T = Y .
Then, we know that by the rank-nullity theorem, dimV = dimX + dimY .
(V,W) such that null T = X and range T = Y .
Then, we know that by the rank-nullity theorem, dimV = dimX + dimY .
I felt so insane solving this, not only because I had no idea what I was doing,
but also because I had typoed the problem description: instead of typing
dimX + dimY = dimV , I wrote dimX + dimY = dimW, which doesn’t make sense
in the context of this problem. I should really look back at the textbook more
T_T
Suppose V is finite-dimensional with dimV > 1. Show that if ϕ :  (V ) → F is a
linear map such that ϕ(ST) = ϕ(S)ϕ(T) for all S,T ∈
(V ) → F is a
linear map such that ϕ(ST) = ϕ(S)ϕ(T) for all S,T ∈ (V ), then ϕ = 0.
(V ), then ϕ = 0.
Suppose that ϕ is a linear map from  (V ) to F such that ϕ(ST) = ϕ(S)ϕ(T) for all
S,T ∈
(V ) to F such that ϕ(ST) = ϕ(S)ϕ(T) for all
S,T ∈ (V ). Whenever I’m not sure how to approach a proof, I will rewrite the
supposition word for word while I desperately try to find purchase.
(V ). Whenever I’m not sure how to approach a proof, I will rewrite the
supposition word for word while I desperately try to find purchase.
Axler says that this is a hint: A subspace ξ of  (V ) is a two-sided ideal of
(V ) is a two-sided ideal of  (V ) if
TE ∈ ξ and ET ∈ ξ for all E ∈ ξ and all T ∈
(V ) if
TE ∈ ξ and ET ∈ ξ for all E ∈ ξ and all T ∈ (V ). Note that the only two-sided
ideals of
(V ). Note that the only two-sided
ideals of  (V ) are
(V ) are  (V ) and
(V ) and 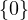 .
.
I’m not entirely sure how I am supposed to use this. Suppose that:
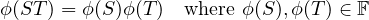
Then, it follows:
| ϕ(ST) | = ϕ(T)ϕ(S) | ||
| = ϕ(S)ϕ(T) by commutativity in F | |||
| = ϕ(TS) |
Say that dim (V ) = n. Then, dimrange ϕ ≤ 1, so:
(V ) = n. Then, dimrange ϕ ≤ 1, so:
dimrange ϕ = dim (V ) - dimnull ϕ (V ) - dimnull ϕ | ≤ 1 by rank-nullity thm. | ||
| - dimnull ϕ | ≤ 1 - dim (V ) (V ) | ||
| dimnull ϕ | ≥ n - 1 |
Totally stuck on this—will need to return later. :(