Theorem 0.1 (Rank-nullity theorem). Given a matrix A, the dimension of the nullspace of A (the nullity) plus the dimension of the column space of A (the rank) equals the dimension of the row space of A.
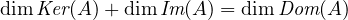
This chapter is exciting because we finally get to one of the theorems at the heart of linear algebra: the rank-nullity theorem.
Theorem 0.1 (Rank-nullity theorem). Given a matrix A, the dimension of the nullspace of A (the nullity) plus the dimension of the column space of A (the rank) equals the dimension of the row space of A.
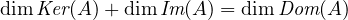
Intuitively, this makes sense if we look at matrices from the point of view of them
being linear transformations. Sometimes, multiplication of a vector  by a matrix
A is written as the function μA
by a matrix
A is written as the function μA . One of the superpowers of matrices is
that they can encode linear transformations of arbitrarily many parameters,
making them useful in just about any applied math situation you can think
of.
. One of the superpowers of matrices is
that they can encode linear transformations of arbitrarily many parameters,
making them useful in just about any applied math situation you can think
of.
The rank-nullity theorem is stating that the dimension of the domain of A (i.e.,
the dimension of the space that the linear transformation’s inputs live in)
is the dimension of the space that these inputs are sent to by the linear
transformation, plus the dimension of the space of the vectors that get sent to 0 by
the transformation, if any. (This is the nullspace, or the kernel of A, which
may be between anything from the trivial 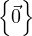 to the entire input space
itself.)
to the entire input space
itself.)
Put even more succinctly, it makes sense that we get what we had originally (pre-transformation) when we add together what we get post-transformation and the vectors that are “lost” during the transformation.
Suppose b,c ∈ ℝ. Define T : 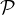 (ℝ) → ℝ2 by
(ℝ) → ℝ2 by
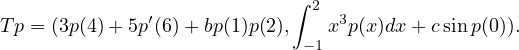
Show that T is linear if and only if b = c = 0.
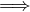 : Assume that T is a linear map. Then the properties of additivity and
homogeneity hold:
: Assume that T is a linear map. Then the properties of additivity and
homogeneity hold:
Additivity: T(u + v) = T(u) + T(v) for all u,v ∈ V
Homogeneity: T(λu) = λT(u) for all λ ∈ F and u ∈ V
So take p,q ∈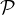 (ℝ). Then:
(ℝ). Then:
| T(p + q) | = Tp + Tq | ||
= 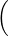 3p(4) + 5p′(6) + bp(1)p(2),∫
-12x3p(x)dx + csinp(0) 3p(4) + 5p′(6) + bp(1)p(2),∫
-12x3p(x)dx + csinp(0)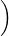 | |||
+ 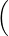 3q(4) + 5q′(6) + bq(1)q(2),∫
-12x3q(x)dx + csinq(0) 3q(4) + 5q′(6) + bq(1)q(2),∫
-12x3q(x)dx + csinq(0) | |||
= 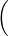 3(p(4) + q(4)) + 5(p′(6) + q′(6)) + b(p(1)p(2) + q(1)q(2)), 3(p(4) + q(4)) + 5(p′(6) + q′(6)) + b(p(1)p(2) + q(1)q(2)), | |||
∫
-12x3p(x)dx + ∫
-12x3q(x)dx + csinp(0) + csinq(0) . . |
By the linearity of integration, we know that ∫
-12x3p(x)dx+∫
-12x3q(x)dx is always
linear. But, the term csinp(0) + csinq(0) is not linear; sinp(0) + sinq(0)≠sinp(0) + q(0).
Therefore, it must be the case that c = 0.
Take p ∈ (ℝ). Then:
(ℝ). Then:
| T(λp) | = λTp | ||
=  3λp(4) + 5λp′(6) + bλ2p(1)p(2),λ∫
-12x3p(x)dx + csinλp(0) 3λp(4) + 5λp′(6) + bλ2p(1)p(2),λ∫
-12x3p(x)dx + csinλp(0) |
In the term bλ2p(1)p(2), it can be seen that λ-→λ2, so b must equal 0. Also,
we know that csinλp(0)≠λcsinp(0) so c = 0, but this was already shown
before.
 : Assume that b,c = 0. Then the map T can simply be written:
: Assume that b,c = 0. Then the map T can simply be written:
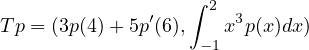
Let’s prove additivity and homogeneity, as this suffices to show that T is a linear
map. Let p,q ∈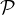 (ℝ):
(ℝ):
| T(p + q) | = Tp + Tq | ||
= 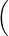 3p(4) + 5p′(6),∫
-12x3p(x)dx 3p(4) + 5p′(6),∫
-12x3p(x)dx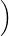 + + 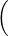 3q(4) + 5q′(6),∫
-12x3q(x)dx 3q(4) + 5q′(6),∫
-12x3q(x)dx | |||
=  3(p(4) + q(4)) + 5(p′(6) + q′(6)),∫
-12x3p(x)dx + ∫
-12x3q(x)dx 3(p(4) + q(4)) + 5(p′(6) + q′(6)),∫
-12x3p(x)dx + ∫
-12x3q(x)dx |
By linearity of integrals, additivity is proven.
For homogeneity, take p ∈ (ℝ):
(ℝ):
| T(λp) | = λTp | ||
= 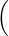 3p(λ4) + 5p′(λ6),∫
-12x3p(λx)dx 3p(λ4) + 5p′(λ6),∫
-12x3p(λx)dx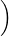 | |||
= 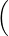 3λp(4) + 5λp′(6),λ∫
-12x3p(x)dx 3λp(4) + 5λp′(6),λ∫
-12x3p(x)dx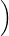 | |||
= λ 3p(4) + 5p′(6),∫
-12x3p(x)dx 3p(4) + 5p′(6),∫
-12x3p(x)dx |
Both directions have been proven.
Suppose T ∈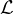 (V,W) and
(V,W) and 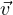 1,…,
1,…,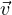 m is a list of vectors in V such that T(
m is a list of vectors in V such that T(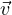 1,…,
1,…,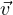 m) is a
linearly independent list in W. Prove that
m) is a
linearly independent list in W. Prove that 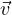 1,…,
1,…,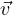 m is linearly independent.
m is linearly independent.
We wish to show that if
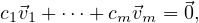
then it must be the case that c1 =  = cm = 0.
= cm = 0.
We know by additivity that
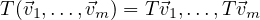
These terms form a linearly independent list, so a linear combination
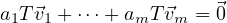
means that a1,…,am all must equal 0. But by linearity this can be written:
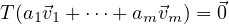
and since we know any linear map T takes 0 to 0, we can assume
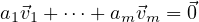
and we know that a1 =  = am = 0, which means that
= am = 0, which means that 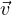 1,…,
1,…,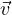 m is linearly
independent.
m is linearly
independent.
Prove that multiplication of linear maps has the associative, identity, and distributive
properties asserted in 3.8.
Suppose T1 ∈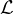 (X,Y ), T2 ∈
(X,Y ), T2 ∈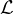 (W,X), and T3 ∈
(W,X), and T3 ∈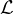 (V,W). Then they all have the
additivity and homogenity properties, and they all map 0 to 0.
(V,W). Then they all have the
additivity and homogenity properties, and they all map 0 to 0.
We prove associativity. Take x ∈ X,y ∈ Y,w ∈ W,z ∈ Z:
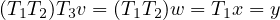
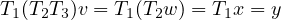
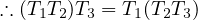
We prove identity. Take T ∈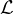 (U,V ) and u ∈ U and v ∈ V :
(U,V ) and u ∈ U and v ∈ V :
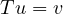
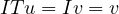
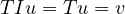
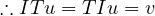
The identity mapping is the linear map that takes every element of an arbitrary
vector space X to itself.
We prove the distributive property. Suppose T,T1,T2 ∈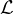 (U,V ) and
D,D1,D2 ∈
(U,V ) and
D,D1,D2 ∈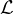 (V,W). Take elements u ∈ U and v,v1,v2 ∈ V :
(V,W). Take elements u ∈ U and v,v1,v2 ∈ V :
| (D1 + D2)Tu | = (D1 + D2)v | ||
| = D1v + D2v | |||
| D1Tu + D2Tu | = D1v + D2u |
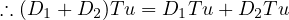
| D(T1u + T2u) | = D(v1 + v2) | ||
| = Dv1 + Dv2 | |||
| = w1 + w2 | |||
| DT1u + DT2u | = Dv1 + Dv2 | ||
| = w1 + w2 |
Give an example of a function ϕ : ℝ2 → ℝ such that
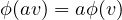
for all a ∈ ℝ and all v ∈ ℝ2 but ϕ is not linear.
Define ϕ to be ϕ(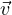 ) =
) = 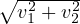 :
:
ϕ(a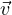 ) ) | = 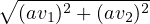 | ||
= a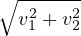 | |||
aϕ(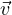 ) ) | = a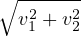 |
Give an example of a function ϕ : ℂ → ℂ such that
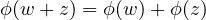
for all w,z ∈ ℂ but ϕ is not linear.
Aside: Problems 9 and 10 together show that checking for homogeneity and additivity
are not enough to show that a map is linear.
Let ϕ : ℂ → ℂ be the function (where w,z ∈ ℂ) ϕ : w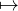 . That is, it sends all
elements of its domain to their complex conjugates. This is not a linear function
(rather, it is antilinear because it is not homogenous. We show its additivity,
nonhomogeneity, and therefore its nonlinearity below.)
. That is, it sends all
elements of its domain to their complex conjugates. This is not a linear function
(rather, it is antilinear because it is not homogenous. We show its additivity,
nonhomogeneity, and therefore its nonlinearity below.)
| ϕ(w + z) | = w + z | ||
| = (a + bi + c + di) | |||
| = (a + c) + (b + d)i | |||
| = (a + c) - (b + d)i |
| ϕ(w) + ϕ(z) | = w + z | ||
| = a + bi + c + di | |||
| = a - bi + c - di | |||
| = (a + c) + (-b - d)i | |||
| = (a + c) - (b + d)i |
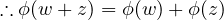
| ϕ(λw) | = λw | ||
| = (c + di)(a + bi) | |||
| = ac + adi + bci + dbi2 | |||
| = (ac - db) + (ad + bc)i | |||
| = (ac - db) + (-ad + -bc)i | |||
| = -bci - adi - db + ac | |||
| = (c - di)(a - bi) | |||
| = λw |
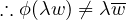
This is also called conjugate homogeneity.
Prove or give a counterexample: If q ∈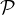 (ℝ) and T :
(ℝ) and T : 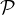 (ℝ) →
(ℝ) →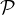 (ℝ) is defined by
Tp = q ∘ p, then T is a linear map.
(ℝ) is defined by
Tp = q ∘ p, then T is a linear map.
This is saying that if T is some transformation mapping the set of all real
polynomials to itself, and is defined by the composition of its input with some
polynomial q, then T is a linear map.
We check for additivity and homogeneity, as usual:
Additivity: Let r,s ∈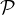 (ℝ). Then, T(r + s) = q ∘ (r + s). Is this equal to
T(r) + T(s)? We check: T(r) + T(s) = q ∘ r + q ∘ s.
(ℝ). Then, T(r + s) = q ∘ (r + s). Is this equal to
T(r) + T(s)? We check: T(r) + T(s) = q ∘ r + q ∘ s.
For a concrete example, let r = x3, s = x, and q = x2. Then, T(r + s) = (x3 + x)2,
and T(r) + T(s) = (x3)2 + x2. Clearly, T(r + s) and T(r) + T(s) is not equal. So, T
cannot be a linear map.
Suppose U is a subspace of V with U≠V . Suppose S ∈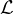 (U,W) and S≠0 (which
means that for some u ∈ U, Su≠0). Define T : V → W by:
(U,W) and S≠0 (which
means that for some u ∈ U, Su≠0). Define T : V → W by:
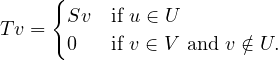
Prove that T is not a linear map on V .
Proof. Say we take an element v ∈ V , and v U, and another element w ∈ V ∩U.
U, and another element w ∈ V ∩U.
Then, v+w ∈ V and v+w U, so T(v+w) = 0. But, Tv = 0 and Tw = Sw, so
Tv +Tw≠0. Since additivity does not hold, T cannot be a linear map on V . __
U, so T(v+w) = 0. But, Tv = 0 and Tw = Sw, so
Tv +Tw≠0. Since additivity does not hold, T cannot be a linear map on V . __
Suppose V is finite-dimensional with dimV > 0, and suppose W is infinite-dimensional.
Prove that 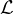 (V,W) is infinite-dimensional.
(V,W) is infinite-dimensional.
Proof. Suppose by contradiction that 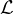 (V,W) is finite-dimensional. That is, the
basis of L(V,W) is of finite length. By the linear map lemma, we know that
given a basis v1,…,vn of V and w1,…,wn ∈ W, there is a unique linear map
T : V → W such that:
(V,W) is finite-dimensional. That is, the
basis of L(V,W) is of finite length. By the linear map lemma, we know that
given a basis v1,…,vn of V and w1,…,wn ∈ W, there is a unique linear map
T : V → W such that:
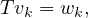
and that 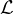 (V,W) is the set of all such T. But note that W is
infinite-dimensional; that is, it has a basis of infinite length. Therefore, according
to the same lemma, there is a unique linear map which maps vk to wk where
wk ∈
(V,W) is the set of all such T. But note that W is
infinite-dimensional; that is, it has a basis of infinite length. Therefore, according
to the same lemma, there is a unique linear map which maps vk to wk where
wk ∈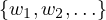 . Each such mapping cannot be expressed in terms of other
mappings; that is what makes it unique. In other words, every mapping is
linearly independent.
. Each such mapping cannot be expressed in terms of other
mappings; that is what makes it unique. In other words, every mapping is
linearly independent.
Then note that there is an infinite amount of linearly independent mappings.
Therefore, they must span a space of infinite dimension. This contradicts our
earlier assumption that 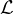 (V,W) had a basis of finite length. Thus,
(V,W) had a basis of finite length. Thus, 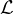 (V,W) is
infinite-dimensional. __
(V,W) is
infinite-dimensional. __
Suppose V is finite-dimensional with dimV > 1. Prove that there exist S,T ∈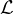 (V )
such that ST≠TS.
(V )
such that ST≠TS.
This is a natural consequence of the fact that matrix multiplication is not
commutative (or perhaps the other way around), but let us prove this with a concrete
example.
Let T ∈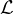 (
( 2(ℝ)) be the transformation that multiplies its input by x2, that
is:
2(ℝ)) be the transformation that multiplies its input by x2, that
is:
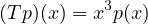
for all x ∈ ℝ.
Let S ∈ (
( 2(ℝ)) be the transformation which differentiates its input:
2(ℝ)) be the transformation which differentiates its input:
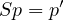
Let q = x2. Then,
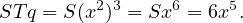
However,
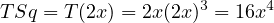
We see that STq≠TSq.